LESSON 03 – SERIES CIRCUITS

WORK EXAMPLE SOLUTIONS

EXAMPLE #1 SOLUTION

Note: This solution re-writes the table after every step in order to help you follow what is going on. Your solution only needs to have the one table with your answers.

We want to solve for all unknowns for the following circuit.

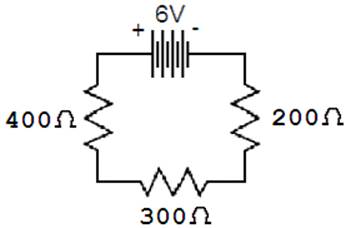
STEP 1 – We start with the table and enter known data.

VT = 6V	IT	RT
V1	I1	R1 = 200Ω
V2	I2	R2 = 300Ω
V3	I3	R3 = 400Ω

STEP 2 – The is only one unknown in the R column so we can solve it.

R_T = R₁ + R₂ + R₃

R_T = 200 W + 300 W + 400 W

R_T = 900 W

Therefore, the total resistance (RT) is 900 ohms.

VT = 6V	IT	RT = 900Ω
V1	I1	R1 = 200Ω
V2	I2	R2 = 300Ω
V3	I3	R3 = 400Ω

STEP 3 – The top row only has one unknown so we can solve for it.

V_T = I_T x R_T

or

I_T = V_T / R_T

I_T = 6 V / 900 W

I_T = 0.0067 A

Therefore, the total current (current leaving source) is 0.0067 A.

VT = 6V	IT = 0.0067A	RT = 900Ω
V1	I1	R1 = 200Ω
V2	I2	R2 = 300Ω
V3	I3	R3 = 400Ω

STEP 4 – There are no rows or columns with a single unknown. So we need to rely on our understanding of series circuits to figure out the next step.

We know that the current is the same everywhere in a series circuit.

So, we know that I_T = I₁ = I₂ = I₃ = 0.0067A

VT = 6V	IT = 0.0067A	RT = 900Ω
V1	I1 = 0.0067A	R1 = 200Ω
V2	I2 = 0.0067A	R2 = 300Ω
V3	I3 = 0.0067A	R3 = 400Ω

STEP 5 – We can now solve the last three unknown voltage values using Ohm’s Law. We will start with V₁.

V₁ = I₁ x R₁

V₁ = 0.0067 A x 200 W

V₁ = 1.3 V

Therefore, the voltage drop over R₁ is 1.3 volts.

VT = 6V	IT = 0.0067A	RT = 900Ω
V1 = 1.3V	I1 = 0.0067A	R1 = 200Ω
V2	I2 = 0.0067A	R2 = 300Ω
V3	I3 = 0.0067A	R3 = 400Ω

STEP 6 – We now solve for V₂.

V₂ = I₂ x R₂

V₂ = 0.0067 A x 300 W

V₂ = 2 V

Therefore, the voltage drop over R₂ is 2.00 volts.

VT = 6V	IT = 0.0067A	RT = 900Ω
V1 = 1.3V	I1 = 0.0067A	R1 = 200Ω
V2 = 2V	I2 = 0.0067A	R2 = 300Ω
V3	I3 = 0.0067A	R3 = 400Ω

STEP 7 – We now solve for V₃.

V₃ = I₃ x R₃

V₃ = 0.0067 A x 400 W

V₃ = 2.7 V

Therefore, the voltage drop over R₃ is 2.7 volts.

VT = 6V	IT = 0.0067A	RT = 900Ω
V1 = 1.3V	I1 = 0.0067A	R1 = 200Ω
V2 = 2V	I2 = 0.0067A	R2 = 300Ω
V3 = 2.7V	I3 = 0.0067A	R3 = 400Ω

We have answers for all unknowns so we are done. We could do an easy verification by checking that VT = V1 + V2 + V3. They are equal so it seems that the work is correct.

EXAMPLE #2 SOLUTION

We need to solve for I₁, I₂ and I₃ in the circuit below. Well, it turns out all of these values will be the same and they will be the same as I_T. So we simply need to solve for I_T.

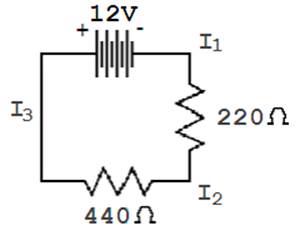
STEP 1 – We will start with the table.

VT = 12V	IT	RT
V1	I1	R1 = 220Ω
V2	I2	R2 = 440Ω

STEP 2 – We can’t solve for I_T yet but we can get R_T.

R_T = R₁ + R₂
R_T = 220 + 440 = 660 W

VT = 12V	IT	RT = 660Ω
V1	I1	R1 = 220Ω
V2	I2	R2 = 440Ω

STEP 3 – We can now solve for I_T.

I_T = V_T / R_T

I_T = 12V / 660 W

I_T = 0.18A

We can now conclude that the current in the circuit is 2.75A.


EXAMPLE #3 SOLUTION

We need to calculate R₃ for the circuit below.

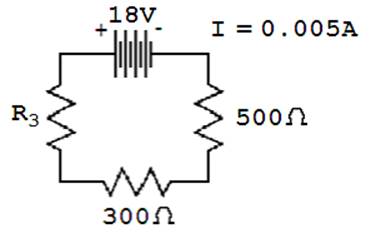
STEP 1 – We will start with the table.

VT = 18V	IT = 0.005A	RT
V1	I1	R1 = 500Ω
V2	I2	R2 = 300Ω
V3	I3	R3 = ?

STEP 2 – We don’t have a way to solve R3 yet. But we can solve for RT using Ohm’s Law.

R_T = V_T / I_T
R_T = 18V / 0.005A

R_T = 3600W

VT = 18V	IT = 0.005A	RT = 3600Ω
V1	I1	R1 = 500Ω
V2	I2	R2 = 300Ω
V3	I3	R3 = ?

STEP 3 – We can now solve for R₃.

R_T = R₁ + R₂ + R₃

3600 W = 500 W + 300 W + R₃

2800 W = R₃

Therefore, R₃ has a resistance of 2800 ohms.