PROJECT 07
– THE FULL ADDER
OVERVIEW
In this
project, we will look at the Full Adder circuit. Using n full adders together, we can add up
two n bit numbers.
For
example, if we want to add up 2 8-bit numbers, we create a circuit that
consists of 8 full adders connected together.
THEORY
Consider
the addition of two binary numbers.
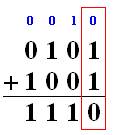
Essentially,
we are adding each column up individually taking into consideration the carry
over from the previous addition.
The
addition of individual columns is what a full adder does.
It has
three inputs - the two numbers in question and the carry over from the previous
addition.
It has two
outputs – the sum that appears at the bottom of the addition and the carry
forward that will be added in the next column’s addition.
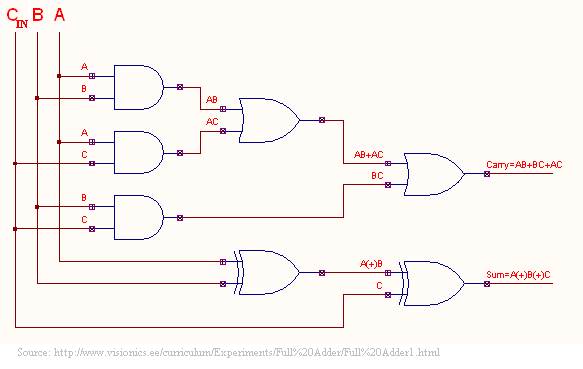
For the
full adder, the inputs are usually labeled A, B and CI (carry in) and the
outputs are usually labeled CO (carry out) and S (sum).
We get the
following truth table for a full adder.
A B CI CO S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
a)
Consider the truth table for S
Notice that
the value of output S is 1 whenever the parity check on the three input bits is
odd. Therefore, this is a parity
checker.
We
therefore know that A XOR B XOR CI = S
b)
Consider the truth table for CO
Notice that
CO is 1 only when one of the following are true:
A AND B (the value of CI doesn’t
matter)
A AND CI (the value of B doesn’t
matter)
B AND CI (the value of A doesn’t
matter)
Therefore,
we can conclude that:
(A AND B) OR (A AND CI) OR (B AND
CI) = CO
CIRCUIT
DIAGRAM
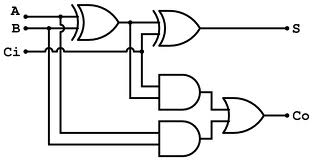
SIMPLIFIED CIRCUIT
DIAGRAM
Here
is a simpler version that expresses part of CO’s circuit using the same XOR
gates as used in S. This reduces the
total number of gates down from 7 to 5.
TASK
Create your
own full adder. Place the LEDs in such a
way that you will be able to read the numbers.
You do not need an LED for the Cin input.
If time
permits, you will connect your adder to another student’s adder. To do this, you need both breadboards to get
their power from one 5V regulator.