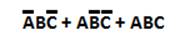LESSON 02 – SUM OF PRODUCTS EQUATIONS

LESSON NOTE

INTRO

When we design a circuit that does a specific job, we generally start with a truth table. From there, we have to convert that truth table into an actual circuit. One way to do this is to use a sum of products equation (SoP equation).

The sum of products equation is really a logical equation form for a truth table. It utilizes AND, OR and NOT Boolean operators. However, we represent AND by a multiplication, OR by an addition and NOT by bar notation (overline).

Just like in math, all letters that are multiplied together are called a term.

EXAMPLE

The following is an example of a sum of products equation:

ĀBC + ABC = Q

It can be read as:

(NOT-A AND B AND C) OR (A AND B AND C) equals Q

There are two terms in the equation above.

Term 1: ĀBC

Term 2: ABC

CONVERTING FROM TRUTH TABLE TO SoP EQUATION

The conversion requires us to consider every row in the truth table that leads to Q=1. We then create a term for each one of those rows. Each term gives a 1 only when the conditions of its row is true. Finally, we add all the terms up to get our sum of products equation.

An example will help explain how all of this works.

EXAMPLE

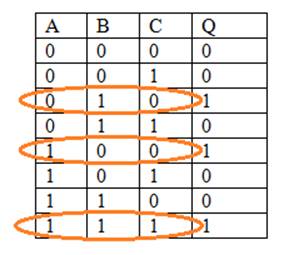
Convert the following truth table to a sum of products equation:




Note: This solution shows more steps than is required in order to help you understand. Most students can write the final sum of products equation directly from the truth table.

SOLUTION

We know that for Q to be 1, we require that

A = 0 and B = 1 and C = 0

or

A = 1 and B = 0 and C = 0

or

A = 1 and B = 1 and C = 1

Alternatively, we can rewrite the statements above without zeros.

= 1 and B = 1 and = 1

or

A = 1 and = 1 and = 1

or

A = 1 and B = 1 and C = 1

We can check if three variables are all 1s by ANDing them together. The result will be a 1 if all three are a 1.

AND B AND

or

A AND AND

or

A AND B AND C

We can now replace the ANDs by multiplication and the ORs by addition

B

+

A

+

A B C

The sum of products equation is therefore

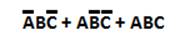
EXPRESSING SoP EQUATIONS AS LOGIC GATE CIRCUIT DIAGRAMS

Using the SoP equation, it is now easy to create a logic gate circuit diagram for any truth table by combining AND, OR and NOT gates.

However, the solutions can be quite long and inefficient.

EXAMPLE

The example below shows a SoP equation and the corresponding circuit diagram.