Java

TOPIC 24 – INTRO TO GRAPHS

LESSON NOTE

GRAPHS

Graphs are structures that are often used in computer science in order to solve advanced programs. It is sometimes hard to tell if a Graph should be used in a solution. Graphs are often useful to discover pathways from one location to another.

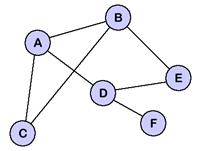
WHAT IS A GRAPH?

A graph is a structure that consists of vertices and edges between some (or all) or the vertices. An edge generally represents a path of travel between the two vertices.

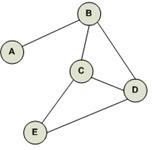
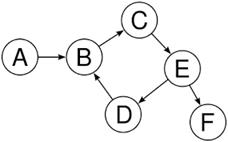
Below are some visual examples:

Example 1
Here, we have a graph with 6 vertices (A, B, C, D, E, F) and 7 edges (AB, AC, AD, BC, BE, DE, DF).

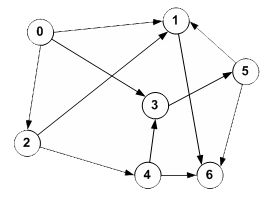
Example 2

This graph has 7 vertices (0 to 6) and 11 edges (01, 02, 03, 12, 15, 16, 24, 34, 35, 46, 56). Notice that the edges have arrow heads. This means that this is a directed graph.

Directed graphs could be used to demonstrate that going from vertex 0 to 3 is possible, but not vice versa (unless we first travelled to 5 and then 1 and then 0).

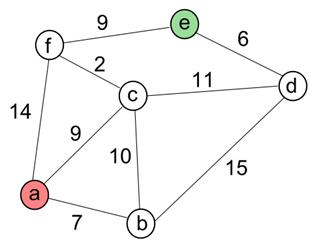
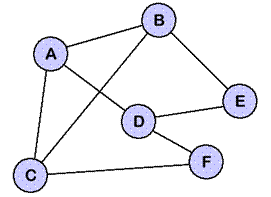
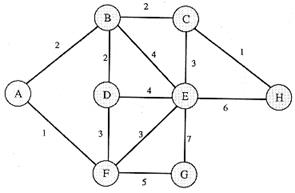
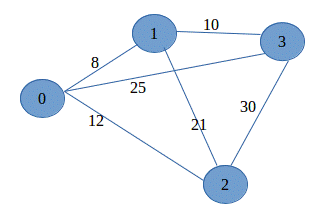
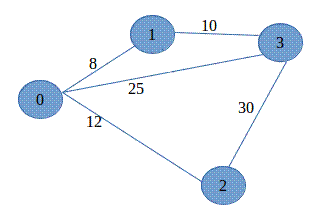
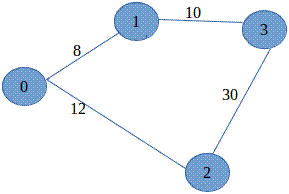
Example 3

This graph includes a weight with each edge. These weights can represent the cost of travelling along that edge. The cost could refer to many things including time required, or distance or perhaps financial cost.

In the example below, we can ask the problem "What is the lowest-cost way to travel from Vertex e to Vertex a? The answer is to travel to f, then to c then to a for a cost of 9 + 2 + 9 = 20. All other possible paths are less cost efficient.

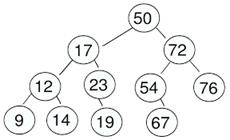
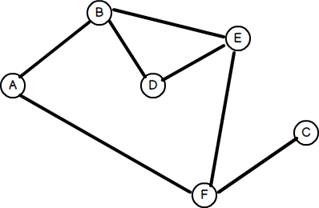
Example 4

The graph below contains no cycles. This is called a tree. Trees are often considered a separate type of data structure from graphs because they can be used for different types of problems. However, really they are just a specialized graph.

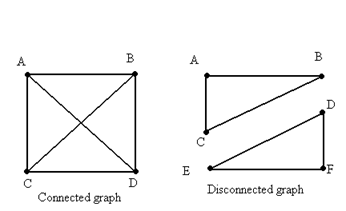
Example 5

The graphs below show the difference between a connected graph and a disconnected graph. As you can see, in disconnected graphs, it is impossible to travel from one location to all others.

TERMINOLOGY

Adjacent – Two vertices are adjacent to one another if they are connected by an edge.

Path – A path is a list of vertices such that each vertex in the list is adjacent to the vertex before and after it.

Degree of a vertex – The degree of a vertex is number of edges that the vertex has connecting it to other vertices. Vertices with a degree of 1 are can only be at the end of paths as they are only adjacent to one vertex.

APPLICATIONS

Graphs can be used in many different fields and areas. Most of the time, they are used to find or study paths between locations or items. Here are a few fields where graphs have been used:

	Electrical circuits Each vertex represents a load. Each edge represent a wire between loads. Weights might represent resistance of the branch.
Real-world Networks Each vertex is a location such as an airport. Each edge shows possible flights. Weights could be time or cost.
	Molecular structures Each vertex could be an atom. Bonds would be represented by edges.
Game Pathfinding Each vertex represents a location that can be moved to. Edges represent pathways that can be followed. If used for NPCs, weights could be used to make odds that NPCs move down certain paths.

TYPES OF PROBLEMS

Most problems that involve graphs involve finding or studying paths between two vertices. We will now consider a few such problems.

TYPE 1 – FINDING ALL PATHS

First, we will look at finding all the possible paths between two vertices. We only consider paths that do not include cycles and never visit a vertex more than once. Such paths are called simple paths.

EXAMPLE PROBLEM #1

Consider the graph below. Give all the possible paths from vertex A to vertex E.

SOLUTION

Here are all the paths that do not include cycles:

ABCE

ABCDE

ABDCE

ABDE

NOTE

If we were to include cycles (which we wouldn't unless specifically asked to), then there would be an infinite number of paths. Here are a few:

ABCE

ABCDBCE

ABCDBCDBCE

and so on…

Note that we are generally only interested in paths that do not contain cycles.

EXAMPLE PROBLEM #2

Consider the graph below. Give all the possible paths from vertex A to vertex E.

SOLUTION

Here are all the paths. Notice how we list them alphabetically to help us make sure we don't miss any.

ABE

ABCFDE

ACBE

ACFDE

ADE

ADFCBE

TYPE 2 – SIMPLE PATH THROUGH ALL VERTICES

We will now look at problems that involve trying to find a path that will visit all vertices in a graph. That is, to find a path that will not visit any nodes more than once.

EXAMPLE PROBLEM #3

Consider the graph below. Is there a simple path that will visit every vertex in the graph?

SOLUTION

We could start with any vertex and simply try to find a path. However, we could simplify our search by making an observation:

Since vertex C is of degree 1, we know that any simple path will have to either start with or end with C. So we can start our search at C.

And we do find two similar paths that works:

CFABDE

CFABED

And those two paths could also be inverted in order to give us two more paths:

EDBAFC

DEBAFC

EXAMPLE PROBLEM #4

Consider the graph below. Is there a simple path that will visit every vertex in the graph?

SOLUTION

Again, analysis helps our search. Vertices A and F are of degree 1. Vertex A will have to be the first vertex in the path and F will have to be the last (notice arrows).

So we:

ABCED and we are stuck and haven't been to F yet

ABDEF and we are stuck and haven't been to D yet

So, there is no way to visit all vertices by following a simple path.

TYPE 3 – LOWEST COST PATH

A common task related to graph problems is to find a path between two vertices. However, it is often required that we find the lowest cost path between them.

EXAMPLE PROBLEM #5

Consider the graph below. What is the lowest cost path between vertex F and vertex C?

SOLUTION

One option is to figure out all possible paths and then calculate their cost. However, you soon realize that you could find one path and then simply try to beat that path with every other option. The advantage of this is that you can stop checking a path as soon as its cost exceeds the best cost you've already found.

Let's say that we do a quick scan and we think the lowest cost path is FEC, after all, it looks like the straightest path. That cost is 3 + 3 = 6.

So, FEC W=6 is the best so far.

Now we try to beat that.

Let's try path FABC. W = 1 +2 +2 = 5. That is the new best path.

No we try to beat that.

When we go through every other possible path, we see that all others have a greater cost than 5. So the lowest cost path is FABC with W=5.

TYPE 4 – SHORTEST PATH TO ALL VERTICES

This type of problem requires that we visit all vertices all while finding the lowest cost path. It may require that we visit a node more than once as well.

EXAMPLE PROBLEM #6

What is the shortest path through all nodes below?

SOLUTION

One can use some analysis to try to find an answer. But it is easy to feel overwhelmed. Thankfully, this graph only has 4 vertices so we can probably do some useful analysis.

First off, we can completely rule out using edges that are longer than two or more edges with the same start and end. For example, the edge 1-2 has a cost of 21 where as edges 1-0 and 0-2 have a total cost of 20. So we will never use edge 1-2.

So we are now left with this:

Again, we can eliminate edge 0-3 with cost 25 as the edges 0-1 and 1-3 have a total cost of 18. Leaving us with:

And now we have a simple problem. The best path will travel to each node but avoid the longest edge which is the edge 2-3 with a cost of 30.

So the path 2-0-1-3 will have a cost of 12+8+10=30.

Unfortunately, we are not able to reduce all graphs that easily. Really, we were lucky to have such a graph.

EXAMPLE PROBLEM #7

What is the shortest path through all nodes?

SOLUTION

This one is more difficult. There aren't any edges to eliminate.

If we analyze well enough, we are able to come up with the best path. But it's hard to do. Plus, it becomes pretty clear that analysis would not be too helpful for a graph with too many more vertices.

So, let's consider every possible path.

1-2-3-4 cost = 75

1-2-4-3 cost = 65

1-3-2-4 cost = 75

1-3-4-2 cost = 70

1-4-2-3 cost = 80

1-4-3-2 cost = 85

2-1-3-4 cost = 55

2-1-4-3 cost = 60

2-3-1-4 cost = 70

2-3-4-1 cost = 85

2-4-1-3 cost = 60

2-4-3-1 cost = 70

3-1-2-4 cost = 50

3-1-4-2 cost = 60

3-2-1-4 cost = 65

3-2-4-1 cost = 80

3-4-1-2 cost = 60

3-4-2-1 cost = 65

4-1-2-3 cost = 65

4-1-3-2 cost = 70

4-2-1-3 cost = 50

4-2-3-1 cost = 75

4-3-1-2 cost = 55

4-3-2-1 cost = 75

So, after checking all 24 paths, we find the two paths (inverse of each other) that have the lowest cost.

TYPE 4B – TRAVELLING SALESMAN PROBLEM

The Traveling Salesman Problem (or just TSP) is a famous computer science problem that involves the finding of the shortest path through all vertices but that also starts and ends at the same vertex.

It has many real-world applications. It's name is a reference to the challenge that sales people have in mapping out their path when visiting different cities (or different locations).

This problem is particularly famous because it is quite easy to understand but finding the best solution for a problem is quite difficult. Certainly, we can just calculate every possible path and find the one with the lowest cost. However, the number of paths is so large that computers aren't close to being fast enough to solve large problems.

The number of possible paths for a fully connected graph with n vertices is n-factorial. So, a graph with 10 vertices has 10-factorial paths which is 3,628,800. That's right, a graph with only 10 vertices has over 3.6 million possible paths that start and end at the same location.

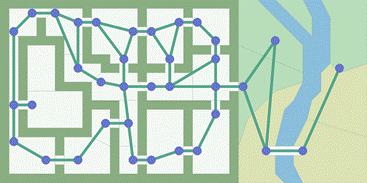
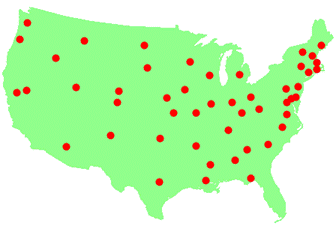
A graph with 20 vertices has 20 factorial possible paths which is 2,432,902,008,176,640,000 or better known as about 2.4 quintillion paths. Don't know what a quintillion is? It's 1000 quadrillions or 1 million trillion. You get the point, this number is crazy! And it's for only 20 vertices!

REAL WORD EXAMPLE

The following TSP problem involves finding the shortest path that goes through all American state capitals (shown below). There are 48 capitals, so 48 vertices. That means there are 48-factorial possible paths.

48! =12,413,915,592,536,072,670,862,289,047,373,375,038,521,486,354,677,760,000,000,000

Or about 12.4 novemdecillion

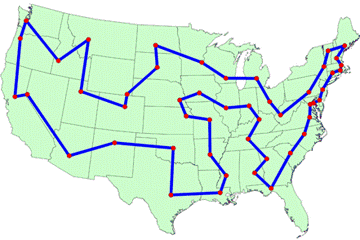
The solution found looked like this:

That's it for now. If time permits, we will revisit the Travelling Salesperson Problem again.